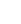As a department, we seek to provide an environment in which students can become mathematical problem solvers who are equipped to pursue challenging careers in our increasingly technological society. Math is an exciting and challenging experience at Big Apple Academy. In all classes students are involved in communication, reasoning, and problem-solving activities. Up-to-date technologies are used to enhance each student’s learning. The goal of the Mathematics Department is to help students become critical thinkers and effective problem solvers while they are mastering a certain body of mathematical knowledge.
Underlying this mission is the belief that the Department must make meaningful use of modern technologies as well as diverse methods of instruction to enhance teaching and learning and increase students’ understanding of mathematical concepts. The Mathematics Department is committed to a mathematics curriculum that is responsive to the needs of its students, and seeks to provide course offerings that present suitable academic challenge, in a supportive environment, based on the expectation that all students can learn mathematics. The mathematics giants of the past would be astonished by the changes the discipline has undergone in recent years. But the ingredients for the success are still the same: logic, creativity, and perseverance. Big Apple Academy’s students will develop these skills through a diverse range of courses: from early development of thinking skills, practical courses of Integrated Math to high level of Algebra and Geometry.
The study of mathematics in the Big Apple Academy schools is aimed at achieving the following goals:
I. In the General direction:
• formation of ideas about mathematics as a part of human culture, the importance of mathematics in the development of civilization and modern society;
• development of ideas about mathematics as a form of description and method of cognition of reality, creating conditions for the acquisition of the initial
experience of mathematical modeling;
• establishment of common methods of intellectual activity, characteristic of mathematics and is the foundation of cognitive culture, meaningful to the various spheres of human activity;
II. In the direction of Personal Development:
• develop logical and critical thinking, culture, language, mental ability to experiment;
• to offer students the intellectual honesty and objectivity, the ability to overcome the mental stereotypes stemming from everyday experience;
• education of personality traits that provide social mobility, the ability to make independent decisions;
• formation of the qualities thought necessary foradaptation to the modern information society;
• development of interest to mathematical creativity and mathematical skills;
III. In the Subject direction:
• mastery of mathematical knowledge and skills necessary to continue their studies in the other high school, college, or other educational institutions,the study of related disciplines, applications in everyday life;
• creating a foundation for mathematical development, the formation mechanisms of thinking characteristic of mathematical activity.
Requirements for learning outcomes and development of course content:
The study of mathematics in our school enables students to achieve the following development outcomes:
I. In the General direction:
1. initial presentation of ideas and methods of mathematics as the universal language of science and technology, a means of modeling the phenomena and processes;
2. ability to see the math problem in the context of problem situations in other disciplines in the life around them;
3. ability to find various sources of information needed to solve mathematical problems, and represents it in an understandable form, make decisions with incomplete and redundant, accurate, and probabilistic information;
4. ability to understand and use mathematical tools visualization (graphs, charts, tables, charts, etc.) for illustration, interpretation, argument;
5. the ability to infer the solution of educational problems and understand the necessity of checking them;
6. the ability to apply inductive and deductive reasoning, see the different strategiesfor solving problems;
7. understanding the essence of algorithmic requirements and the ability to act in accordance with the proposed algorithm;
8. ability to independently set goals, select and create algorithms for solving mathematical problems of education;
9. the ability to plan and implement activities aimed at addressing problems of research character;
II. In the Personal direction:
1. the ability to clearly, accurately, competently express their thoughts orally and in writing; to understand the meaning of problems; to build arguments, to give examples and counterexamples;
2. critical thinking, the ability to recognize logically incorrect statements, distinguish conjecture from fact;
3. the representation of mathematical science as the sphere of human activity, the stages of its development, its significance for the development of civilization;
4. creative thinking, initiative, resourcefulness, activity in solving mathematical problems;
5. ability to control the process and outcome of mathematical learning activities;
6. capacity for emotional perception of mathematical objects, tasks, decisions, reasoning;
III. In the Subject area:
1. mastery of the basic concepts of the main sections of content; presentation of the basic concepts being studied (the number, geometric figure, equation, function, probability) as the most important mathematical model to describe and study the real processes and phenomena;
2. ability to work with mathematical text (to analyze, extract the necessary information), accurately and intelligently to express his thoughts orally and in writing with the use of mathematical terminology and symbols, use the various languages of mathematics, classification, rationale, prove mathematical statements;
3. development of concepts of number and number systems from the natural to the real numbers, the mastery of skills in oral, written, instrumental calculations;
4. acquisition of symbolic language of algebra techniques perform identical transformations, rational expressions, solving equations, systems of equations, inequalities and systems of inequalities, the ability to use the idea of coordinates on the plane for the interpretation of equations, inequalities, systems, ability to use algebraic manipulations, the device equations and inequalities to solve problems from different sections of the course;
5. acquisition system of functional concepts, functional language and symbolism, the ability to use functional graphical representations to describe and analyze real-world relationships;
6. mastery of the basic method of presenting and analyzing statistical data, the presence of ideas about the statistical regularities in the real world and about different ways of learning about stochastic models;
7. the mastery of geometric language, the ability to use it to describe things of the world, the development of spatial concepts and visual skills, skills of geometric constructions;
8. acquisition of systematic knowledge of plane figures and their properties, as well as visual level – about the elementary space bodies, ability to apply systematic knowledge about them to deal with geometric and practical problems;
9. the ability to measure lengths, angles, using formulas for finding perimeter, area and volume of geometric figures;
10. ability to apply learned concepts, results, methods for solving problems of a practical nature and objectives of related disciplines with the need for reference materials, calculator, computer.
 Many people today are concerned about their math abilities. According to a study in the National Library of Medicine, 93% of adults in the United States experience some level of math anxiety. Incorporating math into your child’s daily routine can help them develop a positive relationship with this essential subject.
Many people today are concerned about their math abilities. According to a study in the National Library of Medicine, 93% of adults in the United States experience some level of math anxiety. Incorporating math into your child’s daily routine can help them develop a positive relationship with this essential subject.
Here are ten reasons why math is important for kids to learn.
1. Helps Kids Develop Critical Thinking Skills
As any parent knows, children are naturally curious creatures. They always ask why things are how they are and how they can change. This innate curiosity is what helps children develop critical thinking skills. And there is no better subject for fostering critical thinking than math. Math forces kids to slow down, analyze a problem, and devise a logical solution.
It also encourages them to think outside the box and consider different approaches to a problem. As a result, math can help children develop the essential skills they need to succeed in school and life.
2. Develops a Healthy Brain
A study published in the Journal of Neuroscience has shown that children who engage in regular math activities have healthier brains. It was found that children who regularly solve math problems have increased activity in brain regions associated with attention and focus. In addition, the children showed greater efficiency in neural connections between these regions.
This suggests that math can help children develop a stronger attention span and improve their focus. This can lead to better academic performance and improved cognitive functioning.
3. Teaches Kids How to Handle Failure
In life, there will always be times when we fail. It’s a natural part of the human experience. However, it’s crucial to understand how to deal with failure in a healthy way. Math can teach children how to handle failure in a constructive way. When kids make a mistake while solving a math problem, they can use it as an opportunity to learn and improve their skills. This helps them develop a growth mindset and realize that failure is not the end but simply a part of the learning process.

4. Helps Kids Understand the World Around Them
Math is all around us, whether we realize it or not. It’s a fundamental part of the natural world and plays a vital role in our everyday lives. By understanding math, children can better understand the world around them.
For example, math can help kids understand how long it will take to get somewhere, how much money they need to buy something, or how big or small something is. These are essential skills that children can use in their everyday lives.





5. Encourages Kids to Be Creative
While math may not seem like a creative subject, it encourages children to be creative. This is because math is all about finding different solutions to problems. Students must think outside the box and develop innovative solutions to solve math problems. This process requires them to draw on their imagination and think creatively.
In addition, math can also help children develop their spatial awareness. This is the ability to visualize objects in threedimensional space. Children can develop creative problem-solving skills by understanding how to visualize objects.
6. Teaches Kids How to Make Decisions
Making decisions is a skill that we use every day, often without even realizing it. Interestingly, math can actually help children develop their decision-making skills. This is because math requires kids to weigh different options and choose the best solution.
This process helps them learn to consider all the factors involved in a decision and make choices based on logic. For example, when kids are deciding how to spend their allowance, they need to consider how much money they have and what they want to buy. This decision-making process is an important life skill that math can help children develop.
7. Boosts Self-Confidence
As a parent, you want your child to grow up confident and sure of themselves. You can help them develop these important qualities by enrolling them in a math program. At first, they may balk at the thought of learning equations and dealing with numbers. However, as they begin to master the material, they will start to feel a sense of pride in their accomplishments.
This boost in self-confidence will spill into other areas of their life, and they will begin approaching new challenges with optimism and enthusiasm. Besides, math can also help children develop a sense of perseverance. When they encounter a difficult problem, they will be more likely to stick with it and find a solution.
8. Encourages Kids to Be Persistent
As we mentioned before, math can help children develop a growth mindset. This is the belief that intelligence is not fixed but can be improved with effort. Children with a growth mindset approach challenges with persistence and determination. They understand that failure is not the end but a part of the learning process. This encourages them to keep trying even when they encounter difficulty. As a result, they are more likely to persevere in the face of challenges and achieve success in their lives.
9. Helps Kids Develop Important Life Skills
Though it may not seem like it sometimes, math is an essential life skill, as well. It provides a way of thinking that can apply to everyday situations. For example, basic arithmetic is necessary for budgeting and managing finances. Percentages and fractions are often used in cooking and measurements.
But math isn’t just about numbers, and it also helps to develop important problem-solving and critical-thinking skills. These skills are more important than ever in today’s increasingly complex world. That’s why kids need to build a strong foundation in math from an early age.
10. It’s Fun!
Last but not least, math can be downright fun! There are all sorts of games and activities that can make learning math enjoyable. Many learning apps
and websites make math more engaging for kids. For example, some learning platforms use gamification to make math more enjoyable for kids.
With all these benefits, it’s clear why math is important for kids to learn. A good math program will spark your child’s lifelong love of learning. It will help them develop essential skills they can use in all areas of their lives.
Algebra I: Test Prep & Practice
The Algebra 1 Regents Exam is intended to determine both the knowledge of students and the information taught by educators in the New York public school system. Students must take the Regents Algebra 1 test upon completion of the Algebra 1 course. The NY Regents Exam Algebra I is also a requirement for graduation.
What Is on the Algebra 1 Regents Exam?
The questions on the Algebra 1 Regents Exam come under
4 categories. The 4 categories cover 10 domains. There are
35 questions in total on the exam, in either a multiple-choice or selected-response format. The Number and Quantity category has questions about the domains of The Real Number System and Quantities. The category of Algebra includes questions on the domains of Seeing Structure in Expressions, Arithmetic with Polynomials and Rational
Expressions, Creating Equations and Reasoning with Equations and Inequalities. The next category of Functions contains questions about the domains of Interpreting Functions, Building Functions and Linear, Quadratic and
Exponential Models. The fourth category of Statistics and Probability will consist of questions about the domain of Interpreting Categorical and Quantitative Data.
Number & Quantity
Students taking the Regents Algebra 1 Exam should review reference material about numbers and the properties that apply to them. Between 4 and 10% of exam questions will ask students to figure out the correct answer using their knowledge of numbers and how they can be manipulated. Approximately 1 to 3 test questions will concern the topic of Quantities. Students taking the Algebra 1 Regents Exam should be able to use reasoning skills to respond to questions using quantities.
Algebra
Students taking the Algebra 1 Regents Exam will find that
48-61% of test questions will deal with Seeing Structure in Expressions. In order to solve these problems, students will need to use their knowledge of how to use equivalence. Students should review how to solve equations using polynomials. Test takers will also display their equation writing skills using the information provided on the test. In addition, test takers will use their knowledge of inequalities by showing them on a graph or finding the value of the variable.
Functions
The category of Functions makes up between 24 and 32% of items on the Regents Algebra 1 Exam. In this area, students will be asked to show their understanding and application of functions. Students will be asked to use a set of information to create a function demonstrating the relationship between the quantities. Students will also answer questions by comparing and analyzing each different type of model.
Statistics and Probability
7-15% of exam questions on the Algebra 1 Regents revolve around the knowledge of Interpreting Categorical and Quantitative Data. Students will be expected to solve problems for multiple variables and share their thought processes along the way.
Geometry Regents Study Tips and Tings to Remember_Albert Resources
The Geometry Regents Exam measures a student’s understanding of the Common Core Learning Standards for Geometry. The exam requires that students show an understanding of mathematical concepts, use prior knowledge and prerequisite skills, and solve real world problems using tools and formulas.I’m
The Geometry exam consists of four sections: one multiple choice section and three constructed response sections. Part I of the exam is multiple choice and consists of 24 questions. Each question is worth 2 credits, allowing for a total possible score of 48
The Top 5 Most Common Topics on the Geometry Regents Exam
#1 Most Common Topic: Prove Parallelogram Theorems
#2 Most Common Topic: Congruence and Similarity of Triangles
#3 Most Common Topic: Right Triangles in Application Problems
#4 Most Common Topic: Prove Theorems About Triangles
#5 Most Common Topic: Dilations

The Ultimate Guide to Passing the Geometry Regents Exam Mashup MATH
About AMC , Algebra1 and kangaroo
The AMC 8 provides an opportunity for middle school students to develop positive attitudes towards analytical thinking and mathematics that can assist in future careers.
4th and 5th Grade Contests
Math League’s 4th and 5th grade contests can add interest and excitement to any mathematics program. These are some of the first math contests many students will compete in–and the most fun with math they’ve ever had! All of the questions cover basic 4th and 5th grade topics, including: properties of addition, subtraction, multiplication, and division, time and calendar questions, shapes, perimeter, money, basic ratio and percent, rounding numbers, remainders, integers, and more. These contests challenge students to show their understanding of basic principles through numerical and word problems that encourage an open, flexible approach to problem solving. These contests are provided for intraschool competition, and come with certificates of merit for your school’s high scoring students.
Contest Format: Each contest consists of 30 multiplechoice questions that you can do in 30 minutes. On each 3-page contest, the questions on the 1st page are generally straightforward, those on the 2nd page are moderate in difficulty, and those on the 3rd page are more difficult. The 4th and 5th grade contests are for use in your own school or district. Since results are not used for interschool comparisons, we do not enclose a score report form.
6th, 7th, and 8th Grade Contests
Math League’s 6th, 7th, and 8th grade contests challenge students and schools in interschool league competitions. Students in each league compete for the highest scores, while schools compete for the highest team score: the total of the top 5 scores in each school. Each contest’s questions cover material appropriate to each grade level. Questions may cover: basic topics, plus exponents, fractions, reciprocals, decimals, rates, ratios, percents, angle measurement, perimeter, area, circumference, basic roots, patterns, sequences, integers, triangles and right triangles, and other topics, depending on the grade level. Detailed solution sheets demonstrate the methods used to solve each problem. These contests encourage a variety of problem-solving skills and methods, to improve students’ abilities and understanding of mathematical connections, while having fun!
Contest Format: Each contest consists of 40 multiplechoice questions that you can do in 30 minutes. On each 3-page contest, the questions on the 1st page are generally straightforward, those on the 2nd page are moderate in difficulty, and those on the 3rd page are more difficult. There is a 6th Grade Score Report, and a 7th and 8th Grade Score Report sent to schools in each league after the contest.
Algebra Course 1 Contests
Details Parent Category: Math League Website Published: 17 September 2008
Math League’s Algebra Course 1 Contests are a great way to motivate students learning algebra for the first time. The questions range from basic algebra skills, to more difficult problems, requiring creative solutions by applying algebra course 1 techniques. A wide variety of word problems are included on each contest, in addition to computational problems, to stress the value of applied algebra techniques. These contests are provided for intraschool competition, and come with certificates of merit for your school’s high scoring students, and one of our High School Contest problem books for your school’s top scorer. Here’s a quote from one of last year’s Algebra Course 1 students who participated in our contest: “I hope you keep making those tests. It really gets your brain to work” -Amber L.

Mathematical Kangaroo is an international mathematics competition also known as the Kangaroo math contest. The exam is affiliated with the France- based association kangourou sans frontières and is applied in more than 90 countries.
Designed by academicians and mathematicians, the Kangaroo math competition aims to change the idea of “math is difficult and boring” with attractive, daily life-related, and fun questions.
About Olympiads
Some of the most important benefits of participating in math Olympiads include: Improving Problem-Solving Skills: Math Olympiads involve solving complex and challenging math problems. This helps children develop critical thinking and problem-solving skills, which are important for success in many fields.

About Irina Sterlikova
Irina Sterlikova, Chairperson of the Math Department Mrs. Sterlikova is an educator for whom enthusiasm is not simply a word – it is her motto in education, leadership, and pedagogy. She strongly believes that for students to learn successfully, they must feel inspired. A daring and creative administrator, she is not afraid to think outside the box. Mrs. Sterlikova knows that retaining mathematical knowledge can be an arduous, challenging task for children. Therefore, she always creates math-related events that connect to something festive and extraordinary.
Her philosophy on the teacher-student relationship is that it is a two-way street based on mutual respect and open-minded communication. Mrs. Sterlikova values children’s input into their own education and always encourages her students to be actively involved learners. Sensitive and kind, she keeps her heart open to students’ suggestions and guides them toward academic success in a nurturing, creative, and inspiring fashion.
Mrs. Sterlikova earned her Bachelor of Science degree in Mathematics and Physics from the University of Kazakhstan. She holds a Master of Science degree from the same institution where she took her first steps in teaching. Her 34 years of experience allow her to navigate her administrative duties with great confidence, innovation, and enthusiasm. First, Mrs. Sterlikova began teaching upper high school classes. As she gained more teaching confidence and professional experience, she started teaching college classes. While working as an educator, Irina was also planning and organizing pedagogical activities and professional development opportunities.

Arthur Kats
Arthur Kats’ Education List:
1.Vinnitsa State University, Ukraine, 1993
Major diploma –bachelor’s degree in teaching of Math, Physics and Computer Science.
2.College AHVA Kiriyat-Malachi, Israel, 1996.
Major diploma – bachelor’s degree in teaching of Math and Science. 3. Cope Institute, NY, USA, 2001 AVA certificate
Experience List:
1. Vinnitsa’s High School #6, Vinnitsa, Ukraine 1993-1995
Teaching Math, Physics and Computer Science for grades
9-12
2. Middle School “Yahelim”, Arad, Israel, 1995-2000 Teaching Math and Science for Grades 4-6 2006 – until present time “Big Apple Academy” NY, USA Teaching Math for grades 3-8.

Rima Smolyanskaya
Education:
Kiev State Pedagogical Institute, 1972. Northeastern Illinois University, 1998 Special Education Course.
State of Illinois Certificate in Standard Elementary
Teaching, 2002
National-Louis University, 2002 – 2006
Bachelor of Art in Elementary Education
National-Louis University, 2008
Every Day Math Professional Development
Experience:
Chicago Public School, 1994 – 2017
Teacher of Elementary School, Grade 1-5
Big Apple Academy 2017 – present time
Math Teacher

Tatsiana Radushkevich.
Graduated from Belarusian National Technical University, city of Minsk, Belarus, 2008 year, with the qualification of a combined Bachelor’s and Master’s degree in Technical Teacher Education with a specialization in construction. 3 years after graduation obtained a Teacher of the 2nd Qualification category certification

Yuliya Savenkova
Graduated from Moscow State Open Pedagogical University with a master’s degree in Teacher of Mathematics and Informatics.
Joined Big Apple Academy in 2011 as a classroom teacher and a substitute Math teacher. Now I am a permanent Math Teacher. I am a well-organized and creative person. I do all my best to make lessons interesting for all children, which helps them learn Math better. Present lessons in a comprehensive manner and use visual/audio means to facilitate learning. My goal is to pass Math knowledge to every student. Have an excellent experience of managing conflicts.

Anna Pertseva
Anna Pertseva graduated from Byelorussian State University with major in mathematics.
Anna Pertseva received the Degree of Master of Science Mathematics Education. Her working experience includes Minsk Secondary School #150, Yeshiva She’arit Israel, and 28 years in Big Apple Academy. Anna Pertseva received professional teacher certificate Mathematics 7-12 and Mathematics 5-6 Extension. Anna Pertseva was nominated for recognition in Who’s Who Among America’s Teachers ( 2005-2006 10th Edition) by former student.